LeetCode 671 - 二叉树中第二小的节点
原题链接:https://leetcode-cn.com/problems/second-minimum-node-in-a-binary-tree (opens new window)
# 题目描述
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个。
更正式地说,root.val = min(root.left.val, root.right.val) 总成立。
给出这样的一个二叉树,你需要输出所有节点中的第二小的值。如果第二小的值不存在的话,输出 -1 。
示例 1
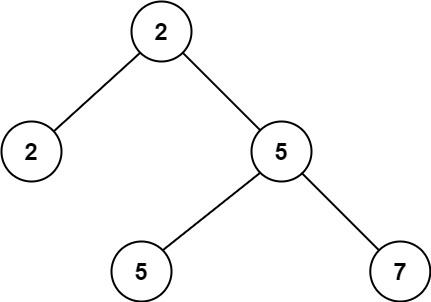
输入:root = [2,2,5,null,null,5,7]
输出:5
解释:最小的值是 2 ,第二小的值是 5 。
示例 2
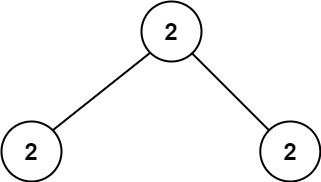
输入:root = [2,2,2]
输出:-1
解释:最小的值是 2, 但是不存在第二小的值。
提示
树中节点数目在范围 [1, 25] 内
1 <= Node.val <= 231 - 1
对于树中每个节点 root.val == min(root.left.val, root.right.val)
# Python题解
# 方法一:深度优先搜索
思路&算法&细节&复杂度
思路
根据题目中的描述「如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个」,我们可以知道,对于二叉树中的任意节点 xx,xx 的值不大于其所有子节点的值,因此:
对于二叉树中的任意节点 xx,xx 的值不大于以 xx 为根的子树中所有节点的值。
令 xx 为二叉树的根节点,此时我们可以得出结论:
二叉树根节点的值即为所有节点中的最小值。
因此,我们可以对整棵二叉树进行一次遍历。设根节点的值为 rootvalue,我们只需要通过遍历,找出严格大于 rootvalue 的最小值,即为「所有节点中的第二小的值」。
算法
我们可以使用深度优先搜索的方法对二叉树进行遍历。
假设当前遍历到的节点为 node,如果 node 的值严格大于 rootvalue,那么我们就可以用 node 的值来更新答案 ans。
当我们遍历完整棵二叉树后,即可返回 ans。
细节
根据题目要求,如果第二小的值不存在的话,输出 -1−1,那么我们可以将 ans 的初始值置为 -1−1。在遍历的过程中,如果当前节点的值严格大于 rootvalue 的节点时,那么只要 ans 的值为 -1−1 或者当前节点的值严格小于 ans,我们就需要对 ans 进行更新。
此外,如果当前节点的值大于等于 ans,那么根据「思路」部分,以当前节点为根的子树中所有节点的值都大于等于 ans,我们就直接回溯,无需对该子树进行遍历。这样做可以省去不必要的遍历过程。
复杂度分析:
时间复杂度:O(n)O(n),其中 nn 是二叉树中的节点个数。我们最多需要对整棵二叉树进行一次遍历。
空间复杂度:O(n)O(n)。我们使用深度优先搜索的方法进行遍历,需要使用的栈空间为 O(n)O(n)。
题解用的是Python3 nonlocal关键字,这里用global替代了一下。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):
def findSecondMinimumValue(self, root):
"""
:type root: TreeNode
:rtype: int
"""
global ans
ans = -1
rootvalue = root.val
def dfs(node):
global ans
if not node:
return
if ans != -1 and node.val >= ans:
return
if node.val > rootvalue:
ans = node.val
dfs(node.left)
dfs(node.right)
dfs(root)
return ans
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 总结
写了挺久没写出来,主要是树的遍历,不了解BFS和DFS。